【CAD/CG笔记】Bezier交Bezier实现思路(二)-处理曲线相切问题
处理错误样例
相切问题
对于常规的曲线求交,通过一阶泰勒展开可以求得交点;但是对于相切的曲线,则无法使用一阶泰勒展开求出切点。
相切时如果使用常规的一阶泰勒展开来做,迭代过程中会出现雅可比矩阵奇异问题导致交点精度无法继续提升,即无法求出满足容差范围要求的交点坐标。
关于分式插值近似迭代
$X(t,s)=x_1(t)-x_2(s)$
$Y(t,s)=y_1(t)-y_2(s)$
牛顿法(一阶泰勒展开,二元泰勒即$x_i(t)$和$y_i(t)$各自的泰勒展开)
$X(t,s) \approx X(t_0,s_0)+X_t’(t_0,s_0)(t-t_0)+X_s’(t_0,s_0)(s-s_0)=0$
$Y(t,s)\approx Y(t_0,s_0)+Y_t’(t_0,s_0)(t-t_0)+Y_s’(t_0,s_0)(s-s_0)=0$
故尝试使用分式插值近似的方式迭代求精(分式有理近似、多点插值)。
$$
X(t,s)\approx \frac {a + b(t-t_0)+c(s-s_0)}{1+A(t-t_0)+B(s-s_0)+C(t-t_0)(s-s_0)}=0
$$
经过实验尝试,选取的六个插值点为:$(t_0, s_0)$,$(t_0 + \delta, s_0 - \delta)$,$(t_0, s_0 - \delta)$,$(t_0, s_0 + \delta)$,$(t_0 - \delta, s_0)$,$(t_0 + \delta, s_0)$,关于插值点的$\delta$的选择,$\delta=1e-6$。
(共有9个候选插值点)
$(t_0 - \delta, s_0 \pm \delta),\ (t_0 + \delta, s_0 \pm \delta),\ (t_0, s_0 \pm \delta),\ (t_0 \pm \delta, s_0),(t_0 , s_0 )$
通过插值点求出$6$个系数$a,b,c,A,B,C$,
$$
\frac {a + b(t-t_0)+c(s-s_0)}{1+A(t-t_0)+B(s-s_0)+C(t-t_0)(s-s_0)}=0
$$
上述分式为$0$即分子式为$0$,故对于$x$和$y$分别得到下式:
$$
a_X + b_X(t - t_0) + c_X(s - s_0) = 0
$$
$$
a_Y + b_Y(t - t_0) + c_Y(s - s_0) = 0
$$
将方程组改写为矩阵形式,于是迭代的更新公式为:
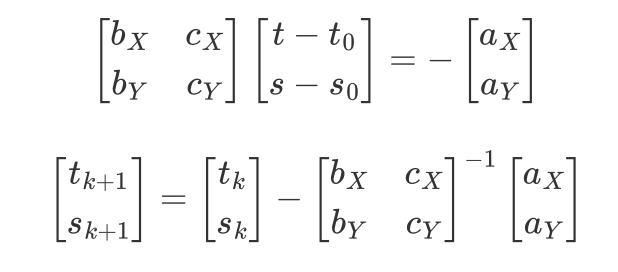
分式插值近似迭代与一阶泰勒展开迭代的对比
本对比重点聚焦于曲线相切时的情况,下面例举出两个例子。
相切例一

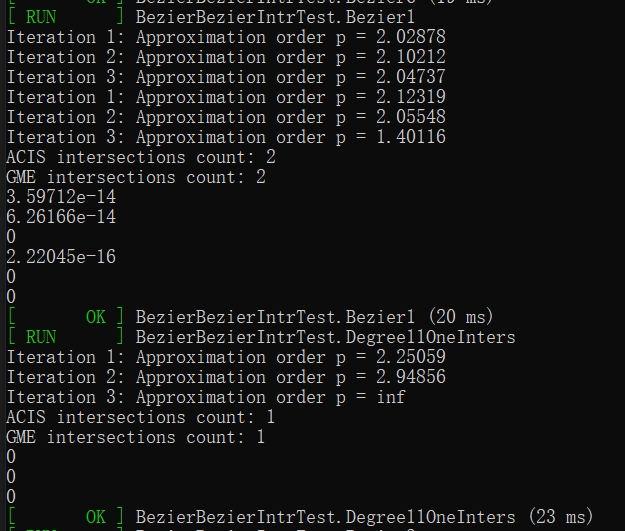
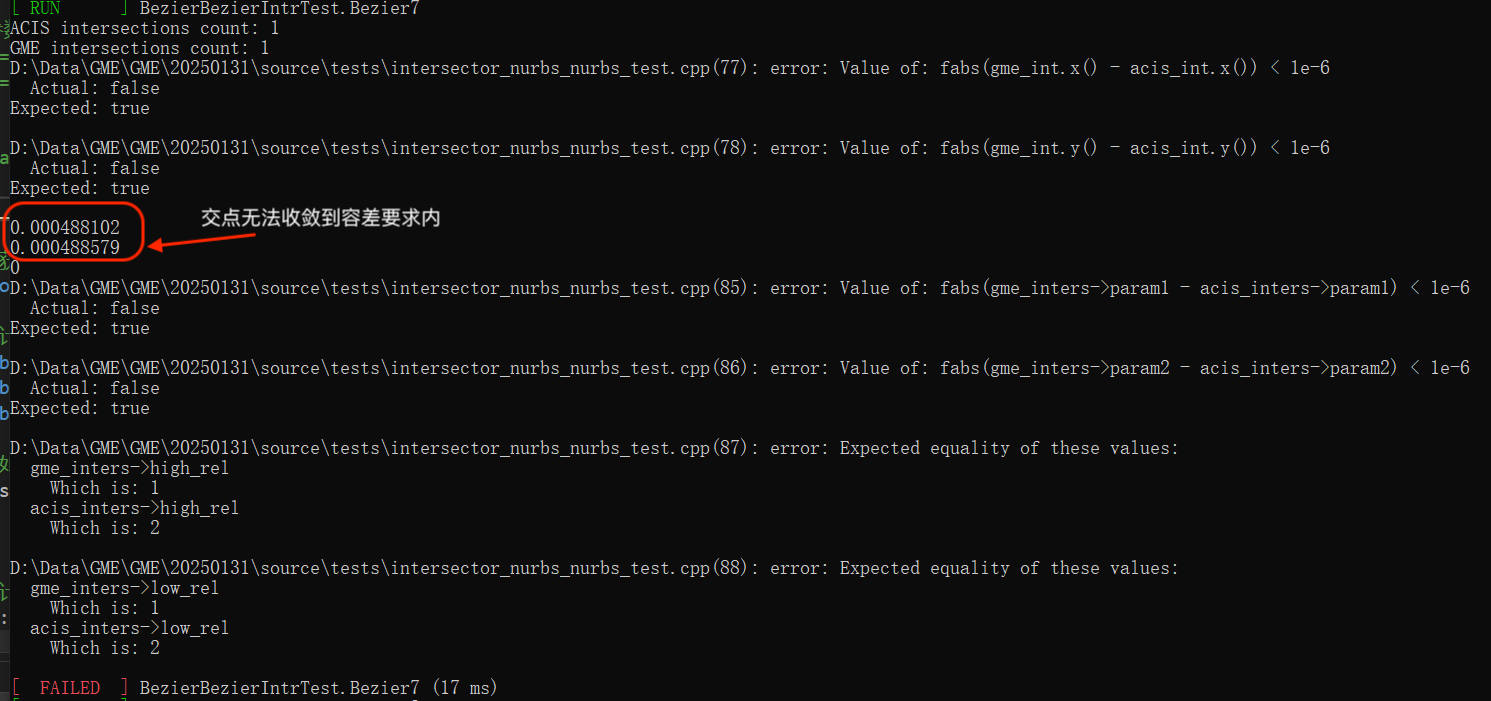
对于这种情况,常规一阶泰勒展开的迭代方法在迭代误差已经达到误差精度要求时,实际交点的精确度仍然没有达到要求。
如下图所示,gme_int变量内存储的值可以看出,即使迭代误差已经小于$1e-6$,交点坐标的误差仍然大于$1e-6$。从而一阶泰勒展开会导致在相切的情况下迭代求精失败。

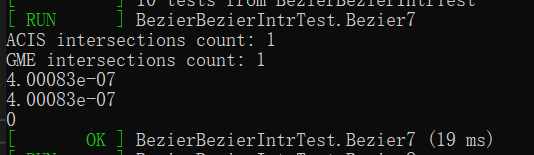
如果使用分式插值迭代,则结果如下,能够将交点坐标求精到容差要求,且收敛阶为$2$。
更换取插值点时的$\delta$为$1e-4$时收敛阶为$3$,如下图。

相切例二

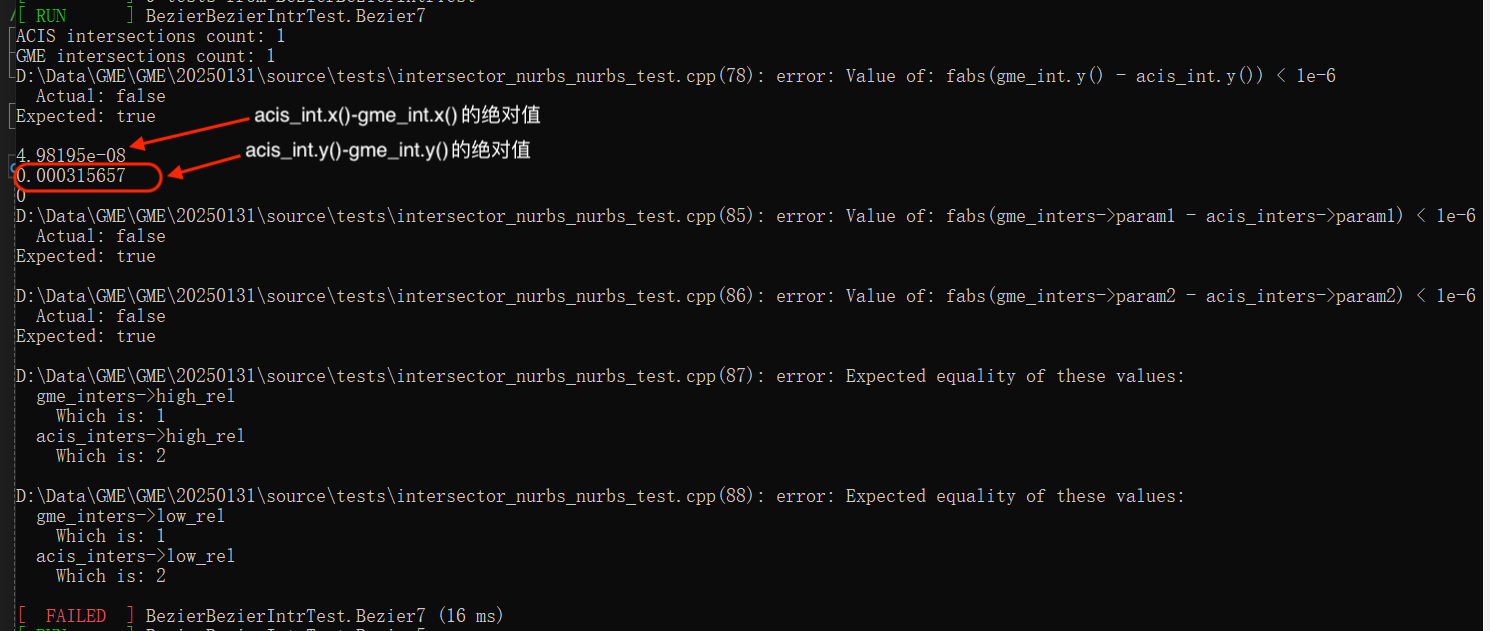
与例一一致。见下图,即使迭代误差已经小于$1e-6$,交点坐标的误差仍然大于$1e-6$。从而使用一阶泰勒展开会导致在相切的情况下迭代求精失败。
用分式插值近似的结果为,
非相切情况
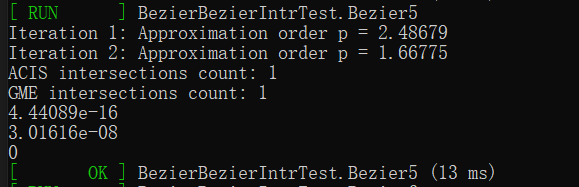
用一阶泰勒展开时收敛阶近似为$2$,如下图,
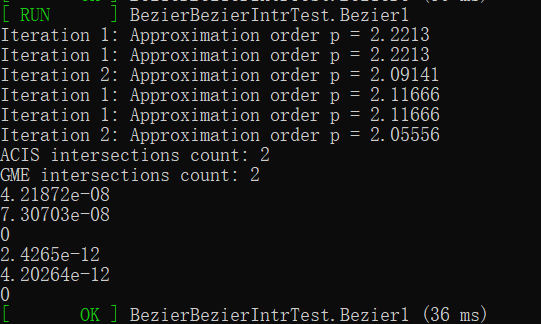
用分式近似时收敛阶也近似为$2$,如下图,